



Next: Many Body Problem
Up: libstokes: Library for Stokesian
Previous: 3D/monolayer d
In the following, physical background is explained.
Fluid is described by Navier-Stokes equation
![$\displaystyle \frac{\partial}{\partial t} \Bigl[ \rho \bm{u} + \left( \bm{u} \cdot \bm{\nabla} \right) \bm{u} \Bigr] = - \bm{\nabla} p + \mu \Delta \bm{u} ,$](img108.png) |
(3.2) |
where 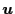 is the fluid velocity,
is the fluid velocity,
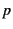 is the pressure,
is the pressure, 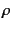 is the density,
and
is the density,
and 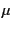 is the viscosity.
The differential operator
is the viscosity.
The differential operator
![$\displaystyle \bm{\nabla} = \left[ \begin{array}{c} \partial/\partial x\\ \partial/\partial y\\ \partial/\partial z \end{array} \right] ,$](img112.png) |
(3.3) |
and 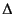 is the Laplacian
is the Laplacian
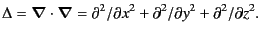 |
(3.4) |
This is the fluid equation of motion, in other words,
the momentum balance equation and the counterpart of
Newton's equation of motion
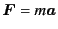 .
Actually, writing the viscous fluid stress by
.
Actually, writing the viscous fluid stress by
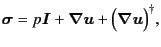 |
(3.5) |
Navier-Stokes equation (3.2) can be written by
the similar equation of motion
![$\displaystyle \frac{D}{D t} \Bigl[ \rho \bm{u} \Bigr] = - \bm{\nabla} \cdot \bm{\sigma} .$](img117.png) |
(3.6) |
The Stokes flows, which is the target of libstokes,
is where the viscous term in Eq. (3.2)
is dominating to the inertial term.
The ratio of the magnitude of these two terms are characterized
by a dimensionless number called ``Reynolds number'' 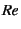
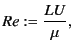 |
(3.7) |
where 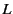 and
and 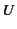 are characteristic length and velocity.
The Stokes flows are the flow of small Reynolds number.
are characteristic length and velocity.
The Stokes flows are the flow of small Reynolds number.
In the limit
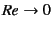 ,
the governing equation of fluids becomes
,
the governing equation of fluids becomes
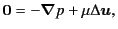 |
(3.8) |
which is a linear partial differential equation.
In the following, we are studying fluid motions
governed by Eq. (3.8)
for incompressible fluid
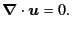 |
(3.9) |
Subsections




Next: Many Body Problem
Up: libstokes: Library for Stokesian
Previous: 3D/monolayer d
Kengo Ichiki 2008-10-12


![$\displaystyle \frac{\partial}{\partial t} \Bigl[ \rho \bm{u} + \left( \bm{u} \cdot \bm{\nabla} \right) \bm{u} \Bigr] = - \bm{\nabla} p + \mu \Delta \bm{u} ,$](img108.png)
![$\displaystyle \bm{\nabla} = \left[ \begin{array}{c} \partial/\partial x\\ \partial/\partial y\\ \partial/\partial z \end{array} \right] ,$](img112.png)
![$\displaystyle \frac{D}{D t} \Bigl[ \rho \bm{u} \Bigr] = - \bm{\nabla} \cdot \bm{\sigma} .$](img117.png)
![]()
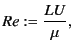
![]() ,
the governing equation of fluids becomes
,
the governing equation of fluids becomes